Tensorflow Tutorial¶
Simple usage example¶
import gnn.GNN as GNN
import gnn.gnn_utils
import Net as n
# Provide your own functions to generate input data
inp, arcnode, nodegraph, labels = set_load()
# Create the state transition function, output function, loss function and metrics
net = n.Net(input_dim, state_dim, output_dim)
# Create the graph neural network model
g = GNN.GNN(net, input_dim, output_dim, state_dim)
#Training
for j in range(0, num_epoch):
g.Train(inp, arcnode, labels, count, nodegraph)
# Validate
print(g.Validate(inp_val, arcnode_val, labels_val, count, nodegraph_val))
Simple toy example for input formatting¶
Input composed by two graphs:
This graphs can be described in the EN Input format.
The E matrix describing the first graph ( [[id_p, id_c, graph_id],...]):
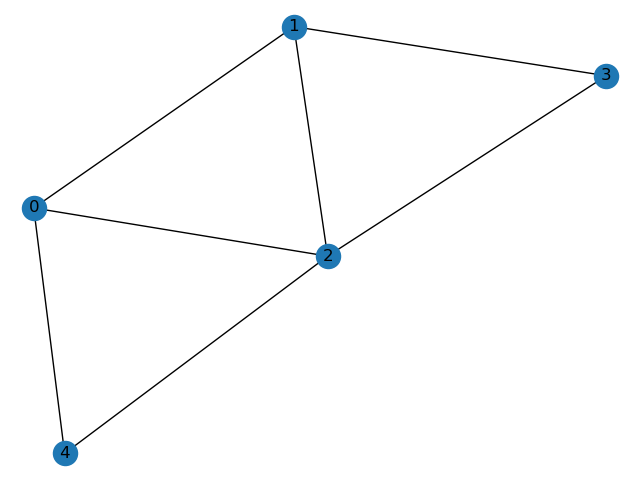
>>> E = [[0 1 0]
[0 2 0]
[0 4 0]
[1 0 0]
[1 2 0]
[1 3 0]
[2 0 0]
[2 1 0]
[2 3 0]
[2 4 0]
[3 1 0]
[3 2 0]
[4 0 0]
[4 2 0]]
Note the last column, denoting the id (0) of the graph to which the arc belongs.
The E matrix describing the second graph:
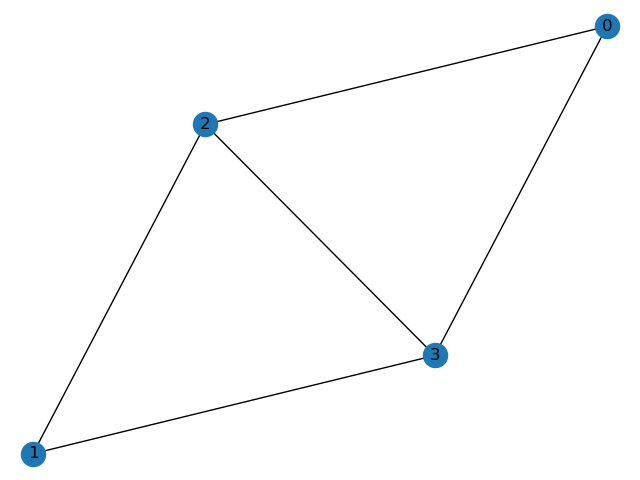
>>> E = [[0 2 1]
[0 3 1]
[1 2 1]
[1 3 1]
[2 3 1]
[2 0 1]
[3 0 1]
[2 1 1]
[3 1 1]
[3 2 1]]
Note the last column, denoting the id (1) of the graph to which the arc belongs .
The global E_tot matrix (with incremental node ids):
>>> E_tot = [[0 1 0]
[0 2 0]
[0 4 0]
[1 0 0]
[1 2 0]
[1 3 0]
[2 0 0]
[2 1 0]
[2 3 0]
[2 4 0]
[3 1 0]
[3 2 0]
[4 0 0]
[4 2 0]
[5 7 1]
[5 8 1]
[6 7 1]
[6 8 1]
[7 5 1]
[7 6 1]
[7 8 1]
[8 5 1]
[8 6 1]
[8 7 1]]
The global N matrix ( in this simple case, each node has a different one-hot feature) ([[node_features, graph_id],... ]) :
>>> N = [[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]]
The from_EN_to_GNN() util takes care of formatting the inputs:
inp, arcnode, graphnode = gnn_utils.from_EN_to_GNN(E_tot, N_tot)
# random labels
labels = np.random.randint(2, size=(N_tot.shape[0]))
labels = np.eye(max(labels)+1, dtype=np.int32)[labels] # one-hot encoding of labels
# set input and output dim, the maximum number of iterations, the number of epochs and the optimizer
threshold = 0.01
learning_rate = 0.01
state_dim = 5
input_dim = inp.shape[1]
output_dim = labels.shape[1]
max_it = 50
num_epoch = 10000
# Create the state transition function, output function, loss function and metrics
net = n.Net(input_dim, state_dim, output_dim)
# Create the graph neural network model
g = GNN.GNN(net, input_dim, output_dim, state_dim)
#Training
for j in range(0, num_epoch):
g.Train(inp, arcnode, labels, count, nodegraph)
# Validate
print(g.Validate(inp_val, arcnode_val, labels_val, count, nodegraph_val))
Description¶
This guide is an introduction to the GNN package.
The implementation consists of the two modules:
GNN.py contains the main core of the GNN
Net.py contains the implementation of several task oriented structures, such as state and output networks, loss functions and metrics definion.
Users may implement their own version of the Net file, for a specific task.
Model definition¶
Input data¶
As described in Matrix-based implementation, the computations are based on the arcs in the input graphs. Hence, inputs to the model must be specified as an ordered edge list.
In particular, for each edge, this structure (inp) must contain:
the id of the child node (used to gather its state)
the father and child node labels
the edge label (if available)
Note
We provide a novel utility to compose this kind of input, given a description of the graph dataset in an E-N format. See section EN Input.
ArcNode¶
In order to aggregate the state per node, a matrix multiplication with an edge–node matrix is performed. The matrix encodes which arcs affect a certain node (see Matrix-based implementation).
This matrix (arcnode) is sparse, to save memory.
NodeGraph¶
This matrix must be defined only in the case of Graph-based problems. See Graph–Based Output function for more information.
We provide a Library to generate these inputs for the simple benchmarks reported in our research papers Examples.
EN Input¶
To simplify the input creation, we provide an utility in the utils.py file, the from_EN_to_GNN(E, N) function.
The user can describe the dataset in the EN format:
- E
numpy array of edges : [[id_p, id_c, graph_id],…]. One row for each arc in the dataset. First column must contain the ids of father nodes, the second column ids of child nodes. The third column contains an id that identifies the graph (to which the node belongs) in the dataset.
- N
numpy array of nodes features - [[node_features, graph_id],… ]. One row for each and every node. A set of columns containing the nodes features. The last column is an id that identifies the graph (to which the node belongs) in the dataset.
The from_EN_to_GNN util takes this two array as input (E N ) and returns the formatted input for the GNN model, inp, arcnode, graphnode.
See Simple toy example for input formatting for a practical example.
State and output function definition¶
The user must define an appropriate version of the Net file for the task to be solved.
In particular, it is possible to define a custom version of the state and output network (MLPs with different architectures, number of layers etc.), loss function and metrics.
More details are available in the Examples section.
Following the notation used in the examples, we import this file into the code with:
>>> import Net_Subgraph as n
Then it is possible to define the net object:
>>> net = n.Net(input_dim, state_dim, output_dim)
where input_dim, state_dim, output_dim represent the dimension of the inputs, the state net and the output net respectively.
Afterwards, the GNN model can be defined using:
>>> g = GNN.GNN(net, input_dim, output_dim, state_dim)
In this way, the model building is complete.
This approach uses some default parameters that can be customized, specifying the complete set of parameters:
>>> g = GNN.GNN(net, input_dim, output_dim, state_dim, max_it, optimizer, learning_rate, threshold, False, param, config,
tensorboard)
Training¶
The Train method runs one epoch of the training procedure:
>>> loss, it = g.Train(inp, arcnode, labels, j)
It receives as inputs, inp, the input matrix described in Input data, the arcnode matrix, the node targets and the current epoch step.
Note
In case of a graph-based task, you can specify the NodeGraph matrix with:
>>> g.Train(inp, arcnode, labels, j, nodegraph)
It returns the loss value loss and the number of iteration of the current step convergence procedure it.
Validation¶
The Validate method performs the validation (i.e., using the validation set) of the model:
>>> loss_val, metr, it =g.Validate(inp_val, arcnode_val, labels_val, j)
It outputs, regarding the set given as input, the loss value loss, the accuracy (custom defined in the Net file) metr, the number of iteration in the convergence procedure it.
Evaluate¶
The Evaluate method performs the evaluation (i.e., using the test set) of the model:
>>> met = g.Evaluate(inp_test, arcnode_test, labels_test)
It gives as output the accuracy on the set given as input, met.
Predict¶
The Predict method can be used to compute the output of each node of the GNN model:
>>> pr = g.Evaluate(inp_test, arcnode_test, labels_test)
It gives as output the output values of the output function (all the nodes output for all the graphs (if node-based) or a single output for each graph (if graph based), pr.